SVD & LSA

方阵的分解

$Ax = \lambda x$

矩阵$A$是$n$维方阵，$x$是$n$维向量，$\lambda$是矩阵$A$的一个特征值，$x$是矩阵$A$的特征值$\lambda$对应的特征向量。计算出特征值和特征向量后，就可以将矩阵$A$进行特征分解，计算所有特征值和对应的特征向量，可以表示为

$A=W\Sigma W^{-1}$

其中$W$是这$n$个特征向量所张成的$n$维方阵，而$\Sigma$是这n个特征值为主对角线的$n$维方阵。

但是，按此方法进行分解，要求$A$必须是方阵，如果不是方阵，则通过SVD进行分解。

SVD分解

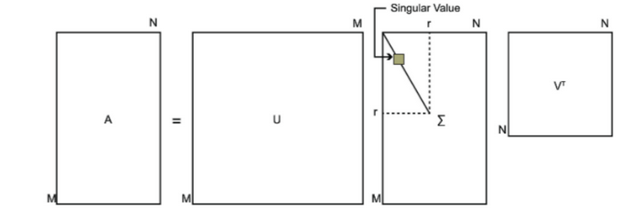
SVD也是矩阵进行分解，但是和特征分解不同，SVD不要求矩阵为方阵，假设矩阵为$m*n$的矩阵，则可以定义SVD分解为

$A=U\Sigma V^{T}$

其中$U$是$m*m$的矩阵，$\Sigma$是$m*n$的矩阵，主对角线上是奇异值，$V$是$n*n$的矩阵，且$U^{T}U=I$，$V^{T}V=I$。

将$V^{T}$和$V$相乘，即可得到一个方阵，因此对其进行特征分解，如下：

$(A^{T}A)u_{i} = \lambda_{i}u_{i}$

此时可以得到对应的$n$个特征值和特征向量，将其张成$n*n$的矩阵$v$，则是上面的$V$矩阵，同理$VV^{T}$可以通过特征分解计算$U$矩阵。

$A=U\Sigma V^{T} =>AV=U\Sigma V^{T}V =>AV=U\Sigma =>Av_{i}=u_{i}\sigma_{i}=>\sigma_{i}=Av_{i}/u_{i}$

通过上式可以求解$\Sigma$

主题模型LSA的例子

目标：有n句话，来从中提取存在可能哪些主题。

每句话用TFIDFVector或者CountVector进行表示，构造稀疏矩阵。比如存在200句话，BOW中存在1024个单词，则可以用矩阵(200, 1024)进行表示，之后对其进行SVD分解，得到U$矩阵(200, 200)表示200个样本，对应了200个topic， $\Sigma$矩阵(200, )表示200个表征topic分数的奇异值和$V$矩阵(200, 1024)表示200个topic对应1024个vocab，这个$V$是经过转置后的。

此时可以取前$n$个奇异值来表征topic的信息，也可以用$V$矩阵的topic所对应的vocab来表征每个topic的关键词。